Astro-Mathematics
Besselian Elements
The Besselian elements are a projection of the Moon shadow axis onto the fundamantal plane which passes through the centre of the Earth and is normal the the centre line of the Sun and Moon.
It uses an X-Y rectangular coordinate system with its origin at the geocenter. The axes of this system are oriented with north in the positive Y direction and east in the positive X direction. The Z axis is perpendicular to the fundamental plane and parallel to the shadow axis. All distances are in units of the Earth’s radius so \(|x| \le 1\) and \(|y| < 1\).
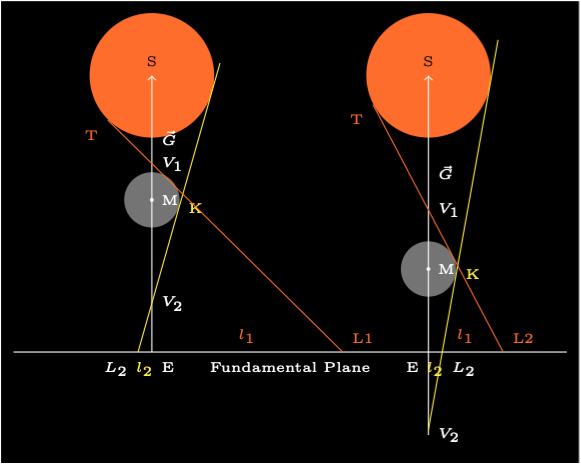
The Figure 1 left diagram shows an annular eclipse. The distance \(l_2\) is the radius of the Moon’s antumbra. The right diagram shows a total eclipse. The distance \(l_2\) is the radius of the Moon’s umbra, it is negative by convention.
-
\(x\) is the x coordinate of the shadow axis.
-
\(y\) is the y coordinate of the shadow axis.
-
\(l_1\) is the radius of the penumbral cone on the plane.
-
\(l_2\) is the radius of the umbral or antumbral cone on the plane.
-
\(d\) is the declination of the shadow axis.
-
\(\mu\) is the Greenwich hour angle of the shadow axis.
-
\(f_1\) is the angle of the penumbral cone \(\widehat{SV_1T}\).
-
\(f_2\) is the angle of the umbral or antumbral cone \(\widehat{MV_2K}\).
There are two constants.
-
\(d_s\) is the radius of the Sun divided by the radius of the Earth.
-
\(d_m = 0.2725076\) is the radius of the Moon divided by the radius of the Earth.
-
\(k=0.272281\) is the radius of the Moon divided by the radius of the Earth for the umbra.
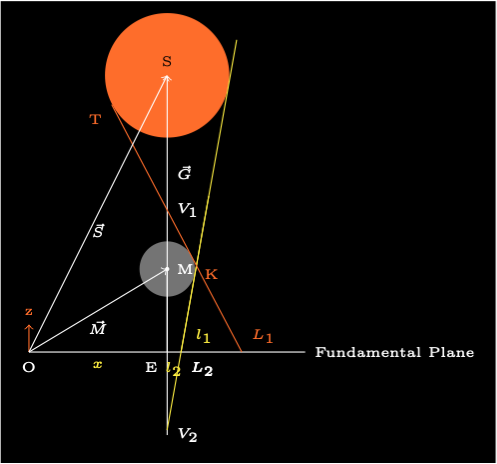
Figure 2 shows more detail got a total eclipse. The point O is the centre of the Earth. The point E is the point where the shadow axis meets the fundamental plane. It will have a y offset. The Besselian elements are labelled in yellow.
For each point on the eclipse path at Julian date t, calculate the geocentric right ascension \(\alpha'\), declination \(\delta'\) and distance \(r'\) of the Sun where the distance is in Earth radii. Also, calculate \(\alpha\), \(\delta\), and \(r\) for the Moon.
Calculate the geocentric cartesian coordinates of the Sun.
\(x_s = r'\cos\delta'\cos\alpha'\)
\(y_s = r'\cos\delta'\sin\alpha'\)
\(z_s = r'\sin\delta'\)
Calculate the geocentric cartesian coordinates of the Moon.
\(x_m = r\cos\delta\cos\alpha\)
\(y_m = r\cos\delta\sin\alpha\)
\(z_m = r\sin\delta\)
The vector \(\vec{S}\) is the geocentric position of the Sun and \(\vec{M}\) is the geocentric position of the Moon. The vector \(\vec{G} = \vec{S} - \vec{M}\) is the vector from the Moon to the Sun. This is normal to the fundamental plane.
The right ascension \(a\) and the declination \(d\) of the Sun from the Moon.
\(\tan a = \frac{G_y}{G_x}\)
\(\sin d = \frac{G_z}{|G|}\)
The coordinates \(x\), \(y\), \(z\) are the intersection of the centre of the Moon shadow in the fundamental plane.
\(x = r\cos\delta\sin(\alpha - a)\)
\(y = r(\sin\delta\cos d - \cos\delta\sin d\cos(\alpha - a))\)
\(z = r(\sin\delta\sin d + \cos\delta\cos d\cos(\alpha - a))\)
The tangents of the umbral cones are calculated from the relative sizes of the Sun and Moon.
\(\sin f_1 = \frac{d_s + d_m}{|G|}\)
\(\sin f_2 = \frac{d_s - d_m}{|G|}\)
The radii of the umbral cones.
\(l_1 = \left( z + \frac{d_m}{\sin f_1}\right)\tan f_1\)
\(l_2 = \left( z - \frac{d_m}{\sin f_2}\right)\tan f_2\)
The Greenwich hour angle \(\mu = \theta - a\) of point E can be calculated from the Earth Rotation Angle at Julian date j where \(\theta = (j - 2451545.0)\).
