Dr Phill’s Science Made Simple

Paul Dirac introduced the bra-ket notation to describe the derivation of amplitudes. The result is always a complex number that is the amplitude.

The bra defines an final condition which is a function that maps a vector to an amplitude.

The ket is a vector defining the initial condition of the event.

It has to be read from right to left!

The probability that a particle will arrive at x, when emitted at the source \(s\), can be represented quantitatively by the absolute square of a complex number called a probability amplitude, in this case, the “amplitude that a particle from s will arrive at x”.

The amplitude itself is a complex number.

When a particle can reach a given state by two possible routes, the total amplitude for the process is the sum of the amplitudes for the two routes considered separately. In the case of two slits.

When a particle goes by some particular route the amplitude for that route can be written as the product of the amplitude to go part way with the amplitude to go the rest of the way. For example the amplitude to go from s to x via hole 1 is equal to the amplitude to go from s to 1, multiplied by the amplitude to go from 1 to x.

Using this notation we can rewrite Equation (5).

Consider an experiment where two particle sources \(A\) and \(B\) are on the \(x\) axis facing each other. There are two moveable detectors at an angle \(\theta\). We need to determine the probability of a particle reaching a detector.

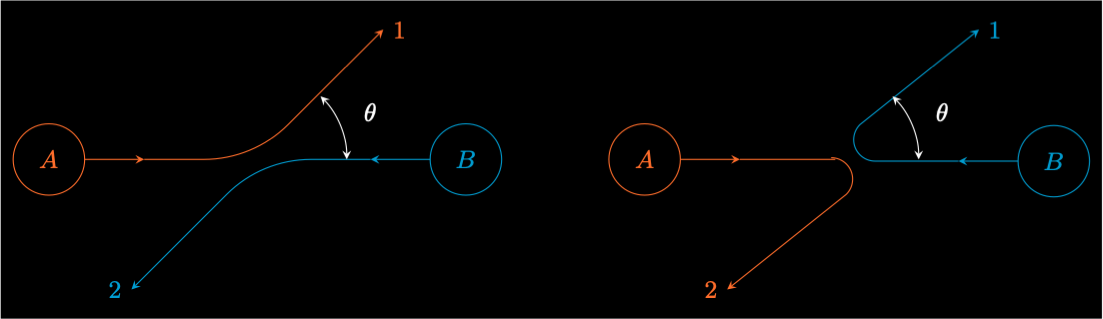
Particle Scattering shows that there are two ways in the which the two particles can scatter.

In an experiment, the particles emitted from \(A\) are alpha particles and the particles emitted from \(B\) are oxygen atoms. Now detector 1 can only detect alpha particles and detector 2 can only detect oxygen atoms. This is the left diagram of Particle Scattering. The amplitude of detecting a particle at either detector is \(f(\theta)\) and the probability is \(|f(\theta)|^2\).

It both detectors can detect both particles then both scattering paths can be detected. Then both types of particle also have an amplitude of \(f(\pi-\theta)\). In this experiment we can’t determine which type of particle has been detected, but we can change the experiment so that we can. So, we have to add the probabilities, not the amplitudes, to get the probability of detecting a particle at a detector.