Dr Phill’s Science Made Simple

Relativity

The Luminiferous Aether

It was long thought that light propagated as a wave through the luminiferous aether. This would mean that light travels at different speeds in different directions due to Earth’s motion in space. In 1881 Albert Michelson tried to measure this difference, called the Aether Wind, with no success. In 1886 Michelson and Edward Morley repeated the experiment with higher accuracy, again with no success. This was perhaps the most important failed experiment!

The absence of the Aether Wind had important consequences. It meant that there is no absolute frame of reference as was previously thought. There is no such thing as an absolute velocity. All velocities can only be measured relative to something else. Distant quasars are active galaxies from the early universe. They are billions of light years away. They are so distant that even if they are travelling at a significant percentage of the speed of light, their motion in undetectable. The motion of the Earth and planets is now made relative to distant quasars to give the nearest thing to an absolute frame of reference.

Oliver Heaviside refined Maxwell’s equations into their modern form. He also calculated that the electric and magnetic fields of a moving electric charge would be deformed. This was a problem as the laws of physics have to be the same for every observer.

In 1892 George FitzGerald and Hendrick Lorentz independently hypothesised that moving bodies have their length contracted in the direction of motion. This explained the issue discovered by Heaviside and the absence of the aether.

Henri Poincaré refined the works of Maxwell and Lorentz and discovered what is now known as Special Relativity.

Lorentz Transformations

Consider two frames of reference K and K'. Think of them as spaceships. Their x axes are aligned and their y and z axes are parallel. Now frame K' is moving at constant velocity v, relative to frame K, in the direction of its x axis. Each frame of reference has an observer stationary within it.

It is important to understand that the speed of light c is the same for every observer, no matter how fast they are travelling.

Each frame has a stationary clock consisting of a tube of length L with a beam of light reflecting back and forth along the tube. The tubes are both parallel to the y axis. Each observer will observe time passing at the same rate due to the speed of light being the same for both. It will take \(\Delta t = 2L/c\) seconds for the light beam to complete a cycle.

Time Dilation

Now the observer in K will see the other observer’s light beam to take a longer time \(\Delta t' = 2l/c\) to complete the cycle.

The path length l of the other light beam can be calculated using Pythagorus' theorem.

\[l^2 = L^2 + \frac{v^2\Delta t'^2}{4}\]

Substitute the values for L and l.

\[\frac{c^2\Delta t'^2}{4} = \frac{c^2\Delta t^2}{4} + \frac{v^2\Delta t'^2}{4}\]

Dividing by \(c^2/4\) and rearranging gives:

\[\Delta t^2 = \Delta t'^2\left(1 - \frac{v^2}{c^2}\right) \\ \Delta t' = \frac{\Delta t}{\sqrt{1 - \frac{v^2}{c^2}}} \\ \frac{d t'}{dt} = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]

The Greek letters \(\beta\) and \(\gamma\) are used as a shorthand notation.

\[\beta = \frac{v}{c} \\ \gamma = \frac{1}{\sqrt{1 - \beta^2}} \\ \Delta t' = \gamma\Delta t \\ \frac{dt'}{dt} = \gamma\]

Thus the observer at K sees the K' clock running slower by a factor of \(\gamma\). The observer in frame K' sees the K clock running slower by a factor of \(\gamma\).

Lorentz Contraction

Now if the clock rod is aligned with the x axis by the observer in frame K', the observer in frame K will measure the length of the rod in frame K as L' and the time taken to complete a cycle is \(t' = 2L\gamma/c\).

When the light beam leaves the end of the tube nearest the K frame, the far mirror is moving so light has to travel a further distance \(L + vt'_1\). So the time taken is \(t'_1 = (L +vt'_1)/c\).

\[t'_1 = \frac{L'}{c + v}\]

Likewise the light beam coming back will have a shorter distance to travel as the mirror is moving towards it.

\[t'_2 = \frac{L'}{c - v}\]

Combining the equations gives:

\[t' = \frac{2L\gamma}{c} = t'_1 + t'_2 = \frac{2L'c}{c^2 - v^2}\]

\[L' = L\sqrt{\left(1 - \frac{v^2}{c^2}\right)} = \frac{L}{\gamma}\]

The observer in K sees lengths in the K' frame in the direction of motion contracted and the observer in K' sees the lengths in the K frame contracted in the direction of motion.

Lorentz Transforms

Consider an event that occurs in frame K at position x at time t. In frame K' the same event occurs at position x' at time t'. In frame K, the distance x' is \(x'\gamma^{-1}\). At time t, the distance between frames if vt.

\[x = vt + \frac{x'}{\gamma} \\ x' = \gamma(x - vt)\]

In frame K', the distance x is \(x\gamma^{-1}\).

\[\frac{x}{\gamma} = vt' + x' \\ x = \gamma(x' + vt')\]

We need \(1 - \gamma^2\) for the next step.

\[1 - \gamma^2 = 1 - \frac{1}{1 - \frac{v^2}{c^2}} = -\frac{\frac{v^2}{c^2}}{1 - \frac{v^2}{c^2}} = -\gamma^2\frac{v^2}{c^2}\]

Eliminate x between the two position equations.

\[x' = \gamma(\gamma(x' + vt') - vt) \\ t = \gamma\left(t' + \frac{vx'}{c^2}\right)\]

Eliminate x' between the two position equations.

\[x = \gamma(\gamma(x - vt) + vt') \\ t' = \gamma\left(t - \frac{vx}{c^2}\right)\]

These are the Lorentz transforms describing the translation from one frame of reference to another when they are moving apart at velocity v in the x direction.

\[t = \gamma\left(t' + \frac{vx'}{c^2}\right) \\ x = \gamma(x' + vt') \\ t' = \gamma\left(t - \frac{vx}{c^2}\right) \\ x' = \gamma(x - vt)\]

Velocity

If the observer in frame K' fires an object in the x direction with velocity u' then the observer in frame K will see the object moving at velocity u. Simple addition of velocities \(u \neq v + u'\) could make u > c which is not allowed.

First, write the Lorentz transforms in differential form.

\[\Delta t = \gamma\left(\Delta t' + \frac{v\Delta x'}{c^2}\right) \\ \Delta x = \gamma(\Delta x' + v\Delta t') \\ \Delta t' = \gamma\left(\Delta t - \frac{v\Delta x}{c^2}\right) \\ \Delta x' = \gamma(\Delta x - v\Delta t)\]

Write u in terms of differentials.

\[\Delta x = u\Delta t \\ \gamma(\Delta x' + v\Delta t') = u\gamma\left(\Delta t' + \frac{v\Delta x'}{c^2}\right) \\ u' + v = u\left(1 + \frac{vu'}{c^2}\right) \\ u = \frac{u' + v}{1 + \frac{vu'}{c^2}}\]

Also, write u' in terms of differentials.

\[\Delta x' = u'\Delta t' \\ \gamma(\Delta x - v\Delta t) = u'\gamma\left(\Delta t - \frac{v\Delta x}{c^2}\right) \\ u - v = u'\left(1 - \frac{vu}{c^2}\right) \\ u' = \frac{u - v}{1 - \frac{vu}{c^2}}\]

To give an example. A spacecraft travelling towards a planet at half of the speed of light launches a probe at half of the speed of light towards the planet. How fast is the probe travelling towards the planet? Newton would add the velocities to give the speed of light. Lorentz gives a different answer.

\[u = \frac{c/2 + c/2}{1 + \frac{c^2}{4c^2}} = 0.8c\]

Now consider that the spacecraft directs a beam of light travelling at the speed of light towards the planet. How fast is the light beam travelling towards the planet? Adding velocities incorrectly gives 1.5c. Lorentz gives:

\[u = \frac{c + c/2}{1 + \frac{c^2}{2c^2}} = c\]

Light always travels at the speed of light no matter what the speed it was emitted at.

Relativity Simplified

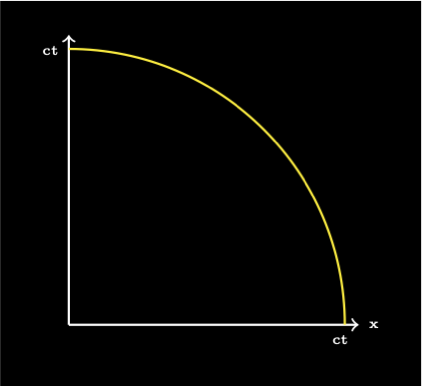
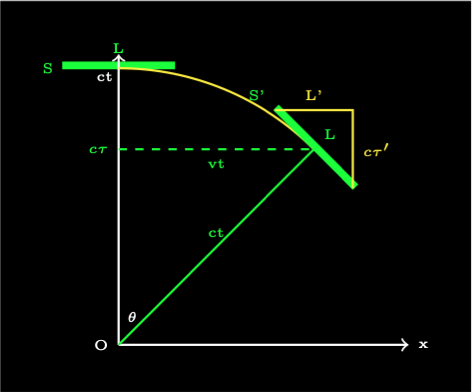
The speed of light \(c\), better called the speed of causality, is the speed that everything in the universe travels at. If an object is at rest in space then it travels at the speed of light through time. If an object has no mass it travels through space at the speed of light and doesn’t experience the passing of time. Every object at time \(t\) must be somewhere on the circular arc of radius \(ct\) in spacetime as shown in the diagram. The horizontal x axis is the direction of motion in space. The vertical axis is time multiplied by the speed of light to make it a distance.

Time Dilation

Now consider a stationary spacecraft of length \(L\). It is always on the arc travelling through time at the speed of light.

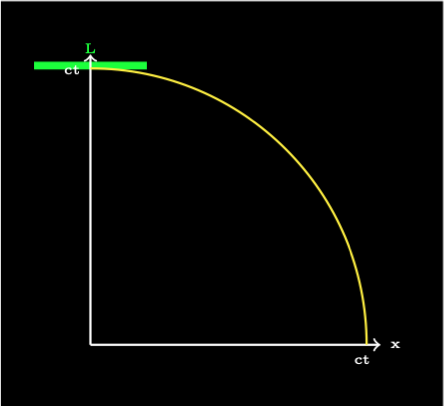
Now show the spacecraft moving at velocity \(v\). It is at a tangent to the arc travelling through spacetime at the speed of light.

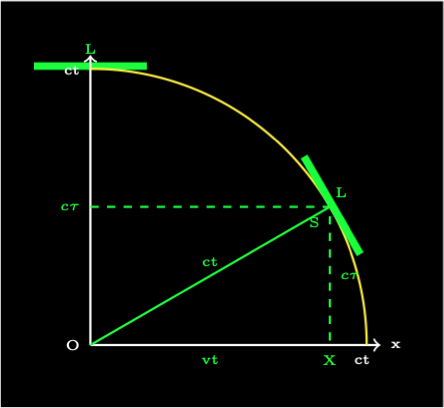
The object is at the top vertex of the right angle triangle \(\widehat{OSX}\). Using Pythagoras' theorum:

\[(ct)^2 = (vt)^2 + (c\tau)^2\]

Divide by the left hand side gives:

\[1 = \frac{v^2}{c^2} + \frac{\tau^2}{t^2}\]

Use the convention of using incremental time \(\Delta t\) and rearrange.

\[\Delta\tau^2 = \Delta t^2\left(1 - \frac{v^2}{c^2}\right) \\ \Delta\tau = \Delta t\sqrt{\left(1 - \frac{v^2}{c^2}\right)} = \frac{\Delta t}{\gamma} \\ \frac{dt}{d\tau} = \gamma\]

This is the time dilation equation! In this case t is coordinate time and \(\tau\) is proper time as experienced on the moving spacecraft.

Length Contraction

Now add a similar right angle triangle with the spacecraft as its hypotenuse.

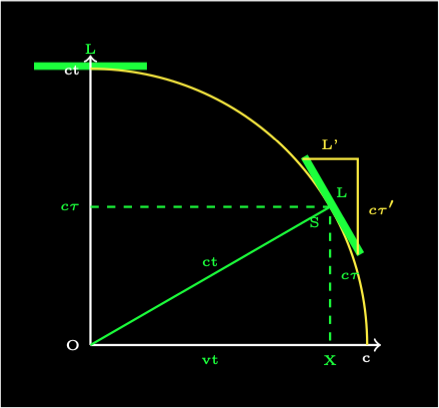
Apply Pythagas' theorum.

\[L^2 = L'^2 +(c\tau')^2\]

Now the moving object is rotated in time and its length appears contracted to \(L'\) to a stationary observer. Using similar triangles:

\[\frac{ct}{L} = \frac{ct'}{L'} = \frac{vt}{c\tau'} \\ c\tau' = L\frac{v}{c}\]

Substitute the value of \(c\tau'\) and rearrange.

\[L'^2 = L^2\left(1 - \frac{v^2}{c^2}\right) \\ L' = L\sqrt{\left(1 - \frac{v^2}{c^2}\right)} = \frac{L}{\gamma}\]

This is the Lorentz length contraction equation!

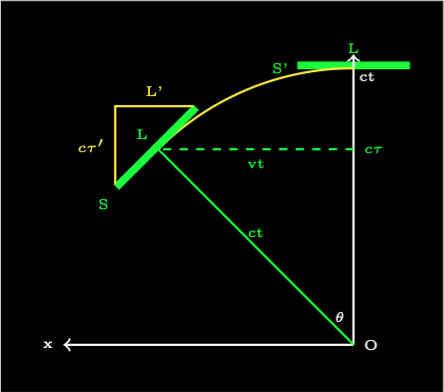
Making Everything Relative

The approach of everything travelling at the speed of light through spacetime helps understanding. There is however the issue that the concept of objects of mass being at rest or moving at the speed of light are meaningless. We can make a modification that a spacecraft S is observing a spacecraft S' travelling away from it at velocity v. No assumption is made about the velocity of spacecraft S other than it is constant.

Lorentz Transformation Matrices

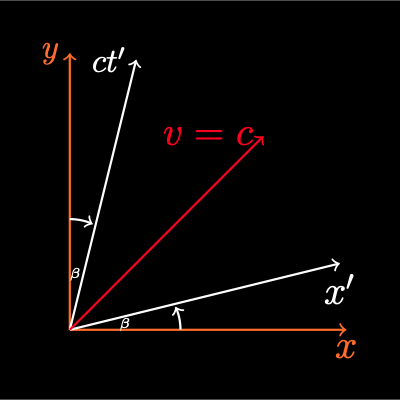
Set \(\beta = \tanh\phi\). Then \(\gamma = \cosh\phi\) and \(\gamma\beta = \sinh\phi\) and rewrite the Lorentz transforms.

\[ct = \gamma\left(ct' + \beta x'\right) = ct'\cosh\phi + x'\sinh\phi \\ x = \gamma(x' + \beta ct') = ct'\sinh\phi + x'\cosh\phi \\ ct' = \gamma\left(ct - \beta x\right) = ct \cosh\phi - x \sinh\phi\\ x' = \gamma(x - \beta ct) = -ct \sinh\phi + x \cosh\phi\]

This can be expressed in matrix form.

\[\begin{bmatrix} ct \\ x \\ y \\z \end{bmatrix} = \begin{bmatrix} \gamma & \gamma\beta & 0 & 0 \\ \gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} ct' \\ x' \\ y' \\z' \end{bmatrix} = \begin{bmatrix} \cosh\phi & \sinh\phi & 0 & 0 \\ \sinh\phi & \cosh\phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} ct' \\ x' \\ y' \\z' \end{bmatrix} \\ \begin{bmatrix} ct' \\ x' \\ y' \\z' \end{bmatrix} = \begin{bmatrix} \gamma & -\gamma\beta & 0 & 0 \\ -\gamma\beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} ct \\ x \\ y \\z \end{bmatrix} = \begin{bmatrix} \cosh\phi & -\sinh\phi & 0 & 0 \\ -\sinh\phi & \cosh\phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} ct \\ x \\ y \\z \end{bmatrix}\]

This is a form of rotation known as a boost. The K' frame’s x' and ct' axes are no longer parallel to the x and ct axes in the K frame.

The length s is invariant under Lorentz transformation. It can also be negated to make the time term positive.

\[s^2 = x^2 + y^2 + z^2 - c^2t^2 = x'^2 + y'^2 + z'^2 - c^2t'^2\]

Henri Poincaré

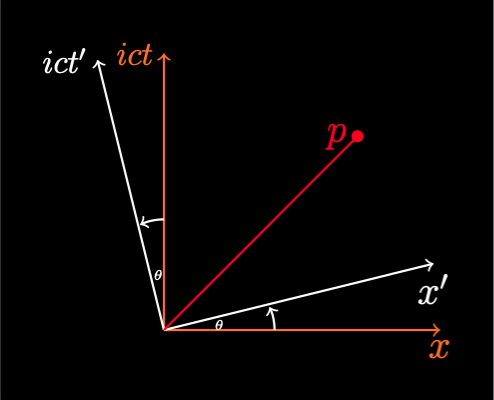
Henri Poincaré discovered from the Lorentz transformations that the quantity \(x^2 + y^2 + z^2 - c^2t^2\) is constant. He realised that introducing imaginary time ict as a fourth spatial coordinate made a Lorentz transformation a simple rotation in four-dimensional space. He thought that it would be too much effort to extend the ideas of four-dimensional geometry.

This is unfortunate as imaginary time makes a lot more sense and is rarely taught. It requires that \(\beta = \frac{iv}{c}\).

\[\beta = \frac{iv}{c} = i\tan\theta\\ \gamma = \frac{1}{\sqrt{1 + \beta^2}} = \cos\theta\\ t = \gamma\tau\]

The Lorentz transformations become:

\[ict = \gamma\left(ict' + i\beta x'\right) = ict'\cos\theta - x'\sin\theta \\ x = \gamma(x' + \beta ct') = ict'sin\theta + x'\cos\theta \\ ict' = \gamma\left(ict - i\beta x\right) = ict\cos\theta + x\sin\theta\\ x' = \gamma(x - \beta ct) = -ict\sin\theta + x\cos\theta\]

This can be expressed in matrix form.

\[\begin{bmatrix} ct \\ x \\ y \\z \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} ct' \\ x' \\ y' \\z' \end{bmatrix} \\ \begin{bmatrix} ct' \\ x' \\ y' \\z' \end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta & 0 & 0 \\ -\sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} ct \\ x \\ y \\z \end{bmatrix}\]

These are now rotation matrices.

Special Relativity

Henri Poincaré and Hendrick Lorentz exchanged letters discussing and refining the Lorentz transformations. Poincaré wrote two papers in 1900 describing what he later called the principle of relativity. This states that no experiment can distinguish between a state of uniform motion and a state of rest.

The principle can be explained by a thought experiment. Alice and Bob are two astronauts in separate spacecraft. Bob is moving away from Alice at a constant velocity that is a significant percentage of the speed of light.

Special Relativity is only valid if there is no acceleration. So the initial condition has to be that Bob accelerated away from Alice to reach his final velocity, or that Alice accelerated away from Bob!

Alice observes that her spacecraft is its usual length and that her clock is ticking at the usual rate. Bob observes that his spacecraft is its usual length and that his clock is ticking at the usual rate. When Alice observes Bob’s spacecraft, she sees that its length is contracted in the direction of travel and that his clock is running slower than hers. Bob also sees that Alice’s spaceship is length contracted and her clock is ticking slower than his!

Albert Einstein

In 1905 Albert Einstein published a paper on what is now known as Special Relativity. He derived the Lorentz Transformations from the two principles of relativity.

The laws of physics are the same for all observers.
The speed of light is the same for all observers.

Unusually the paper did not reference any other person’s work. He was aware of most of the papers written by Lorentz and Poincaré.

He also published a paper of mass-energy equivalence \(E=mc^2\). It is now clear that Einstein plagiarised Poincaré’s work. He did however view the work from a different perspective and interpretation that led to the general theory.

Poincaré never acknowledged Einstein’s work on relativity - he died in 1912 before the general theory was published.

Einstein acknowledged that Poincaré laid the foundations for relativity decades after Poincaré’s death.

Conclusion

Length contraction and time dilation have been observed and validate the theory of Special Relativity. There is, however, an important restriction on Special Relativity. The effects are only valid if the observers are in inertial frames. If an observer experiences acceleration then Special Relativity is no longer valid during the period of acceleration.

A curious consequence of this is that Special Relativity and General Relativity are incompatible. General Relativity states that if spacetime is curved, there must be an acceleration.

Special Relativity is also compatible with Quantum Theory. The Dirac equation is an important part of Quantum Theory. It is based on Spinors which encapsulate the Lorentz transforms.