Relativity
Time Dilation
Sir Isaac Newton believed that time passes at the same rate everywhere. The theories of Special Relativity and General Relativity state that time passes at different rates for different observers. Differences in the rate that time passes is referred to as time dilation. There are actually two different causes of time dilation.
We need different ways of measuring time. Coordinate time \(t\) is the rate that time passes by a clock a long distance away from any masses. It always passes at the same rate. Now we define an observer who’s clock ticks at a rate \(t_0 \ge t\). The observer is stationary for example at a fixed location on the Earth’s surface. Next we define a traveller who is in a different location to the observer and may be moving at a fixed speed with respect to the observer. Proper time, denoted by the Greek letter Tau \(\tau\), is the rate that the traveller’s clock ticks as compared to the observer’s clock. In general it runs slower than the observer’s time and coordinate time, so \(\tau \ge t_0 \ge t\), and in extreme circumstances it can become infinite and proper time stops.
Both the observer and traveller will always see their own clocks ticking at the same rate. The observer may see that the traveller’s clock is running slower than his or hers. Should they ever meet and compare clocks, the traveller’s clock would show an earlier time.
Parameters
There are a number of parameters that are required for time dilation calculation.
-
The gravitational constant \(G\) is difficult to measure and is not known to high accuracy.
-
The mass of the Earth \(M\) is difficult to measure and is not known to high accuracy.
-
The standard gravitational parameter of Earth \(\mu = GM = 3.986004418\cdot 10^{14} m^3s^{-2}\) is known to a much higher accuracy than \(G\) and \(M\).
-
The speed of light \(c\) is defined to be exactly \(299792458.0 ms^{-1}\)
The Schwarzschild radius \(r_s\) defines the smallest radius that a massive object can be compressed into. If a massive object is smaller than this, it is a black hole and time stops at the event horizon at \(r = r_s\).
For the Earth \(r_s = 8.87 mm\), about the size of a marble.
The orbital speed \(v\) of an object in orbit at radius \(r\) from the Earth’s centre is:
Examples
We will calculate the time dilation for a number of different applications.
-
An aircraft flying at an altitude of 10,000 metres at 900 km/hour (250 m/s).
-
Concorde flying at an altitude of 18,000 metres at 2,140 km/hour (595 m/s).
-
The International Space Station (ISS) orbiting at an altitude on 400 kilometres, orbital speed 7668 m/s.
-
A GPS satellite orbiting at an altitude of 20,180 kilometres, orbital speed 3,874 m/s.
-
A Geostationary satellite orbiting at 35,785 kilometres, orbital speed 3,074 m/s.
Special Relativity
The Lorentz transformations define a form of time dilation associated with moving at speed. The transformation for an object moving at velocity \(v\) is:
Where \(\tau\) is the time measured on the traveller’s clock as seen by the observer relative to \(t_0\), the time measured on the surface of the Earth. We will measure the time dilation experienced by traveller for each second passing on the Earth surface. So, \(t_0 = 1\) and we subtract it from \(1\) to give the time dilation \(\delta\tau\). The value is negative as the traveller’s clock ticks slower than the observer’s clock. As the value is very small we will multiply by \(10^{12}\) to give the time dilation in picoseconds per second.
The calculated values for the applications due to speed are:
-
Aircraft -0.35 ps/s.
-
Concorde -1.96 ps/s.
-
ISS -327 ps/s.
-
GPS -83 ps/s.
-
Geo -52 ps/s.
General Relativity
The closer you get to a massive object, such as the Earth, the slower time passes. The Schwarzschild outer solution to the General Relativity Field Equations gives the time dilation at a distance \(r\) from the centre of the Earth.
As before, we can define the time dilation in picoseconds per second.
The Earth’s surface at sea level is at a radius of \(R = 6378 km\). The time dilation due to gravity at sea level is \(695 ps/s\). The clock of a traveller at any altitude above sea level ticks faster than the observer’s clock. So, the time dilation due to gravity is positive.
The calculated values for the applications due to gravity are:
-
Aircraft 0.09 ps/s.
-
Concorde 1.99 ps/s.
-
ISS 41 ps/s.
-
GPS 528 ps/s.
-
Geo 590 ps/s.
Gravitational time dilation has been measured between two atomic clocks where one clock is one metre above the other!
Total Time Dilation
The total time dilation of a traveller is the sum of the gravitational time dilation and the velocity time dilation. The velocity time dilation, particularly due to orbital speed, only makes sense for altitudes above sea level. Gravitational time dilation can be calculated for locations inside the Earth using the Schwarzschild interior solution.
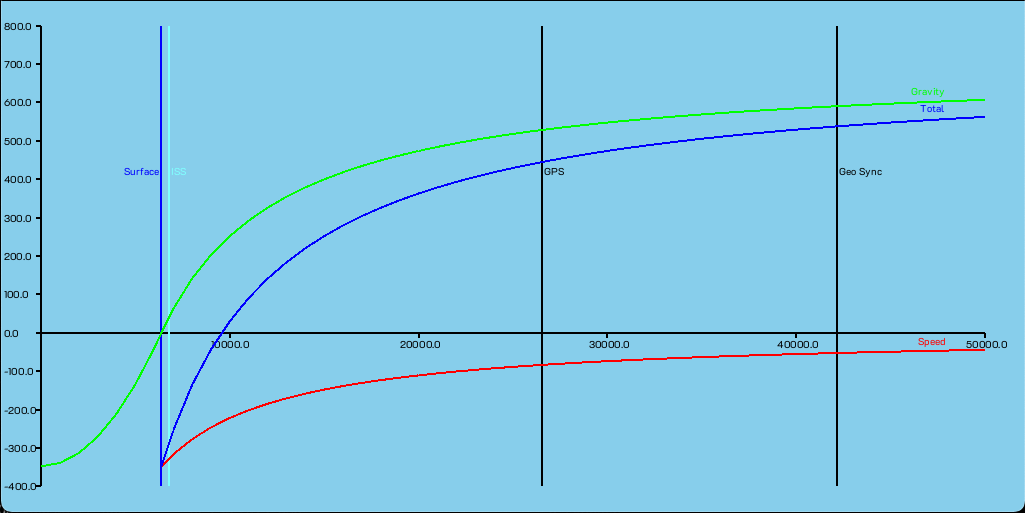
Earth Time Dilation shows the time dilation components relative to an observer on the Earth’s surface. The gravitational time dilation at the Earth’s surface is 695.35 pico seconds per second slower than for a clock a large distance from Earth.
-
The horizontal axis shows radius from the Earth’s centre in kilometers.
-
The first vertical line shows the Earth radius 6378.1366 km.
-
The second vertical line shos the ISS orbit 400 km altitude.
-
The third vertical line show the GPS satellite orbits 20,180 km altitude.
-
The final vertical line show the Geostationary orbit 35,785 km altitude.
-
The vertical axis shows time dilation in picoseconds per second.
-
The red line shows an orbiting object’s velocity time dilation relative to the observer.
-
The orange line shows an object’s gravitational time dilation relative to the observer.
-
The black line shows the total time dilation of an orbiting object relative to the observer.
The calculated total values for the applications' time dilation are:
-
Aircraft 0.74 ps/s.
-
Concorde 0.02 ps/s.
-
ISS -286 ps/s.
-
GPS 445 ps/s.
-
Geo 537 ps/s.
A passenger on an aircraft will age slightly faster than on the ground. This has been verified by taking one of a pair of synchronised atomic clocks on a long haul flight and comparing the two clocks on return.
Concorde passengers at its highest altitude and speed would have experience almost no time dilation.
Clocks on the ISS run slower than clocks at sea level. This amounts to about 4.5 ms over six months.
A clock on a satellite in GPS orbit runs faster than at clock at sea level. Although the effect looks small, it is however a serious issue. Each location transmission from a GPS satellite contains a transmission time. To maintain the required GPS location accuracy, the GPS clocks must be accurate to 30 nanoseconds. Time dilation would cause GPS clocks to gain 30 nanoseconds every 67 seconds! The atomic clocks on GPS satellites are slowed down to compensate for time dilation.
A clock on a satellite in Geostationary orbit runs faster than at clock at sea level. If clocks are required to high accuracy then time dilation needs to be compensated for.
The time dilation is zero when the two components cancel out. This happens for an orbit at 9559 km from Earth’s centre that is an altitude 3181 km, which is about half an Earth radius.
International Atomic time, French Temps Atomique International (TAI), is a high-precision atomic coordinate time standard based on the rate of proper time on Earth’s geoid. The geoid is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth’s rotation, if in the absence of the influences of winds and tides. TIA is the weighted average of the time measured by over 450 atomic clocks housed at over 80 institutions world wide. As each atomic clock is at a different altitude, their output needs to be corrected for gravitational time dilation. UTC = TIA - 37 seconds due to an initial 10 second time difference in 1972 and 27 leap seconds added to UTC since 1972.
