Astrophysics
Coordinates
When working with astronomical objects, several different coordinate systems are used. It is important to understand what these coordinate systems are and how to transform between them. There are three coordinate systems required for calculations. Each has its own coordinate axis system and positions are described using spherical coordinates. The spherical coordinate angles have different names in each coordinate system. Each system is defined by a plane that is inclined at an angle to the other systems. Angles are not all measured from the same axis or in the same direction.
Ecliptic Coordinates and Equatorial Coordinates
The plane of the ecliptic is a commonly used coordinate base as the important bodies of the solar system orbit close to this plane. There are also equatorial coordinates based on the plane of the Earth’s equator. The ecliptic plane is so called because eclipses occur when the Sun and Moon align in the plane.
The intersection of the ecliptic and equatorial planes is the Vernal Equinox. The direction of the Vernal Equinox is known accurately for epochs such as J2000 (2000-01-01T12:00:00). The equinox precesses, so at any given time the direction is the equinox of date.
The angle between the ecliptic and equatorial planes is the Earth’s axial tilt \(\epsilon\). It is about \(23^\circ 26'\) and also precesses.

-
\(P\) and \(P'\) are the celestrial poles.
-
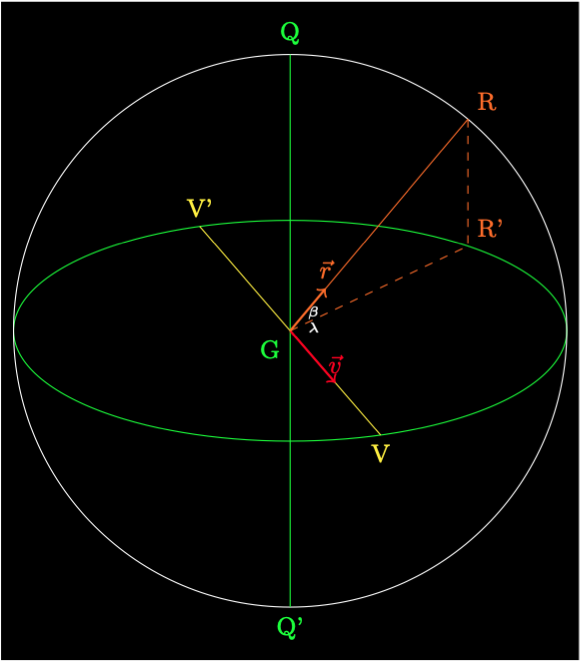
\(Q\) and \(Q'\) are the ecliptic poles.
-
\(S\) and \(S'\) are the solstices.
-
\(V\) and \(V'\) are the equinoxes.
-
\(VUV'U'\) is the celestrial or equatorial plane.
-
\(VSV'S'\) is the ecliptic plane.
The unit vectors \(\vec{v}\), \(\vec{u}\), and \(\vec{p}\) form an orthogonal equatorial axis system. The unit vectors \(\vec{v}\), \(\vec{s}\), and \(\vec{q}\) form an orthogonal ecliptic axis system.
There is an inverse transformation.
Ecliptic Coordinates
Consider an astronomical body at point \(R\). The projection of \(R\) onto the ecliptic plane is \(R'\). The unit vector direction to \(R\) from the centre of the Earth \(G\) is \(\vec{r}\). The ecliptic longitude is \(\lambda = \widehat{VGR'}\). The ecliptic latitude is \(\beta = \widehat{R'GR}\).
Equatorial Coordinates
Consider an astronomical body at point \(R\). The projection of \(R\) onto the equatorial plane is \(R'\). The unit vector direction to \(R\) from the centre of the Earth \(G\) is \(\vec{r}\). The right ascension is \(\alpha = \widehat{VGR'}\). The declination is \(\delta = \widehat{R'GR}\).

Horizontal Coordinates
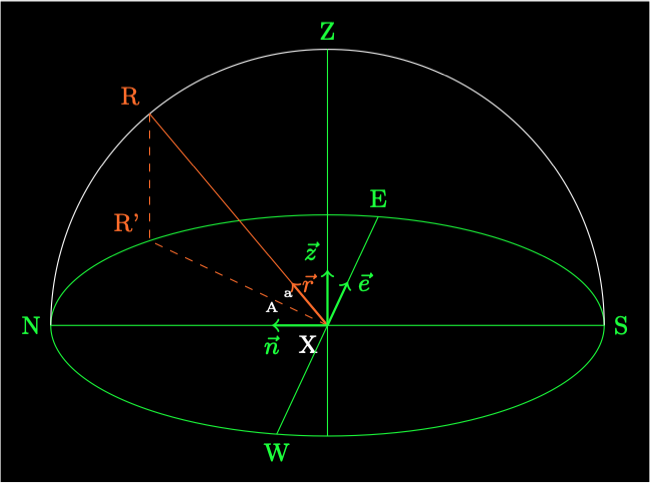
Consider an observer at point X with a horizon plane NSEW at longitude \(\theta\), latitude \(\phi\).
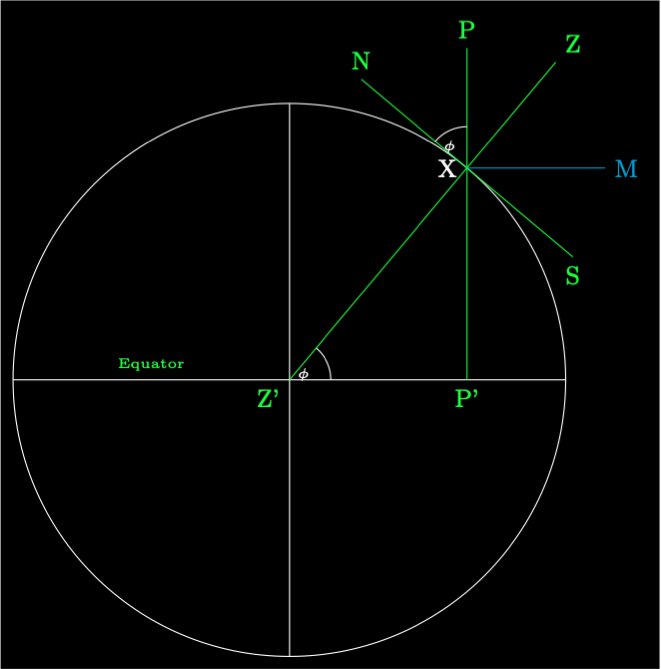
The projection of \(R\) onto the ecliptic plane is \(R'\). The unit vector direction to \(R\) from the centre of the Earth \(G\) is \(\hat{r}\). The azimuth is \(A = \widehat{NXR'}\). The altitude \(a = \widehat{RXR'}\). The point directly overhead is the zenith \(Z\). The unit vectors \(\hat{e}\), \(\hat{n}\), and \(\hat{z}\) form an orthogonal horizontal axis system.
Relate the position to the angles.
The zero rotation angle in Equatorial and Ecliptic coordinates is defined by the direction of the Vernal Equinox. The zero angle of Azimuth is defined to be when the meridian passes the Vernal Equinox. The time that this occurs used to be known as Greenwich Apparent Sidereal Time (GAST). It is now known as the Earth Rotation Angle (ERA).
A sidereal day is the time interval that a meridian on the Earth passes the Vernal Equinox twice. This is about 23 hours 56 minutes. The ERA needs to be calculated to set the zero of Azimuth for a given day correcting for the precession of the equinoxes.
For a Julian Date \(J\) calculate the time since J2000. The ERA \(\theta(t_U)\) in radians can be calculates using a linear series.
Meridian Passing
We need to determine a suitable coordinate frame for the observer at \(X\). This can be defined using three unit vectors. The polar vector \(\hat{p}\), the meridian vector \(\hat{m}\), and the normal to the meridian place \(\hat{n} = \hat{p}\wedge\hat{m}\).
The meridian vector’s position is time dependent due to the rotation of the Earth. For any given day, the Julian date of midday is \(J_m\). The Julian date of local noon is \(J_n = J_m - tz\), where \(tz\) is the local timezone offset in days.
Now, calculate Julian date of solar noon.
Where \(E\) is the Equation of Time in minutes for the day. At Solar noon the Sun is at culmination. Calculate the right ascension of the Sun \(\alpha_s\) at \(J_s\) as a reference direction.
Calculate the right ascension of the object \(\alpha_r\) at solar noon. The observer needs to rotate through an angle \(\alpha' = \alpha_r - \alpha_s\) for the object to culminate. This will occur at julian date \(J = J_s + \alpha'/2\pi\). If \(J > J_n + 0.5\) it is in the next day so \(J \rightarrow J - 1\).
We can now calculate the right ascension of the meridian at time \(J\).
We can now calculate the unit vectors at location \(X\) at time \(J\).
At the time of meridian passing, the object must lie in the meridian plane \(\hat{n}\cdot\hat{r} = 0\).
If the object is moving like the Moon or a satellite, then iteration is required. Replace \(J_s\) with the calculated meridian passing time. Limit the number of iterations to 5. The are some days when no meridian passing occurs. This happens within a few days of a full moon. The iterations will alternate between the start of the day and the end of the day. If after iteration the object dies not lie in or very close to the meridian plane then there is no meridian passing for that day.
Right Ascension and Declination to Azimuth and Altitude
In equatorial coordinates, an event occurs at right ascension \(\alpha\), declination \(\delta\) at Julian date \(J\). An observer is at longitude \(\theta\) and latitude \(\phi\). The event needs to be converted to the observer’s horizonal coordinates azimuth \(A\) and altitude \(a\).
The hour angle \(h\) corrects the right ascension of the event by the observer’s longitude \(\theta\). The ERA \(\theta(t_U)\) is also required.
The azimuth and altitude can be calculated using coordinate transformations.
