Astrophysics
Eclipses
An eclipse or syzygy occurs when three bodies are aligned. We are fortunate that the Moon is about 1/400th of the diameter of the Sun, and the Sun is about 400 times further from the Earth than the Moon. This means that when aligned, the Moon can cover the bright surface of the Sun revealing the beautiful solar corona in a total eclipse of the Sun.
Solar eclipses can only occur at a New Moon. There are four types of solar eclipse.
A partial eclipse is when the Moon covers part of the Sun. These occur when the Moon is slightly North or South of the ecliptic plane. Some years have four partial eclipses. The other types of solar eclipse always start and end as partial eclipses.
An annular eclipse occurs when the Sun and Moon are aligned when the Moon is near its apogee. The Moon’s disk isn’t big enough to completely cover the Sun.
A total eclipse occurs when the Sun and Moon are aligned and the Moon completely covers the Sun’s surface. The path of totality is a narrow band several hundred kilometers wide in an arc between sunrise and sunset. Outside of the band of totality a partial eclipse can be seen.
A hybrid eclipse is total for part of its path and annular for the rest.
Annular, hybrid, and total eclipses are called central eclipses. Each year typically has either two central eclipses or four partial eclipses.
Lunar eclipses occur when the Sun, Earth, and Moon align and the Moon falls completely in the Earth’s shadow. They can only occur at Full Moon. They can be full or partial. A lunar eclipse is visible from the whole hemisphere facing the Moon. There are two lunar eclipses in each year.
When Mercury or Venus are aligned so that they can be seen passing over the Sun it is called a transit. Transits of Venus occur in pairs that are eight years apart. There is a 121.5 year gap between pairs of transits. The last pair were 8 June 2004 and 5/6 June 2012. The next transit will be 10/11 December 2117. Transits of Mercury are more frequent with 13 or 14 occuring each century. The last one was 11 November 2019. The next one will be 13 November 2032.
Moon Orbital Periods
There are several ways of defining the period of a lunar orbit. Three of these periods need to be aligned for an eclipse to occur.
The synodic month is the time between successive New Moons. It averages 29 days 12 hours and 44 minutes. A solar eclipse can only occur close to New Moon, and a lunar eclipse can only occur close to Full Moon.
The anomalistic month is the time it takes for the Moon to move from perigee to the next perigee. It averages 27 days 13 hours and 19 minutes. A total solar eclipse can only occur when the Moon is close to perigee.
The Moon’s orbit is inclined at about 5° to the plane of the ecliptic. The points where the orbit intersects the ecliptic are called nodes. There is an ascending node and a descending node. A draconic month is the time it takes for the Moon to pass between successive ascending nodes, or descending nodes. I averages 27 days 5 hours and 5 minutes. An eclipse can only occur when the Moon is close to a node. It is called a draconic month because it was thought that there were dragons at the nodes that eat the Sun.
Eclipse Seasons
An eclipse can only occur when the Moon is close to a node when the Earth, Sun, and Moon align. There are two eclipse seasons each year when the line between nodes is pointing towards the Sun. An eclipse season is about 35 days. Some years, a third eclipse season can start in December.
Twice every year the Sun crosses the line connecting the nodes. Given that the ecliptic longitude of a node is \(\lambda_n\) and the ecliptic longitude of the Sun is \(\lambda_s\). The Sun crosses a node on the day when \(\lambda_s = \lambda_n\). An eclipse season starts 17 days before node crossing and ends 17 days after node crossing. There will be at least one New Moon and at least one Full Moon during an eclipse season, each will have an eclipse.
If a New Moon occurs around the middle of an eclipse season there will be a central solar eclipse. There can be two New Moons in the same eclipse season. In this case they will both be partial eclipses. If a Full Moon occurs around the middle of an eclipse season there will be a lunar eclipse.
Solar Eclipses
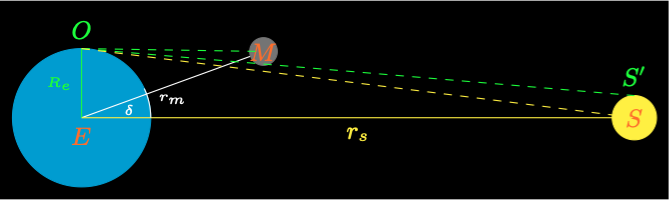
Figure 1 shows how to calculate the minimum conditions required for an eclipse, given that the ecliptic longitude of the Sun \(\lambda_s\) and the ecliptic longitude of the Moon \(\lambda_m\) are the same or at \(180^\circ\) to each other at a New Moon or Full Moon.
-
The point \(S\) is the centre of the Sun, \(E\) is the centre of the Earth, and \(M\) is the centre of the Moon.
-
The point \(O\) is the observer on the surface of the Earth.
-
The distance \(R_s\) is the radius of the Sun and \(r_s\) is the distance from the Sun to the Earth.
-
The distance \(R_m\) is the radius of the Moon and \(r_m\) is the distance from the Earth to the Moon.
-
The distance \(R_e\) is the radius of the Earth.
We need to determine the maximum ecliptic latitude of the Moon \(\delta = \widehat{SEM}\) for an observer at \(O\) to see a partial eclipse. This means that the line \(OS'\) from the observer at \(O\) touches the lower limb of the Moon and the upper limb of the Sun at \(S'\). Given that the angles are all less than \(5^\circ\), we can dispense with the trigonometric functions as \(\sin\theta \approx \theta, \cos\theta \approx 1\).
The angular radius of the Sun is \(\rho_s = \widehat{SOS'} = R_s/r_s\).
The angular radius of the Moon is \(\rho_m = \widehat{S'OM} = R_m/r_m\).
The parallax angle of the Moon for the observer is \(\delta_m = \widehat{EMO} = R_e/r_m\).
As the angular radius of the Earth from the Sun \(\widehat{ESO}\) is very small, the angls \(\widehat{EOS}\) is almost \(90^\circ\).
We now have the condition for a solar eclipse to be visible somewhere on the Earth’s surface. A solar eclipse will occur the condition is true at a New Moon.
\(|\delta| < \delta_m + \rho_s + \rho_m\)
We need to determine the conditions for a total or annular eclipse.
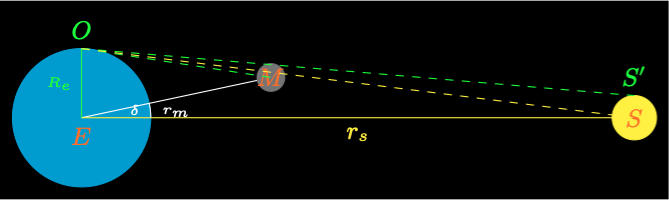
Figure 2 shows the minimum conditions for a total or annular solar eclipse.
An annular solar eclipse occurs if \(\rho_m < \rho_s\) and the following condition holds.
\(|\delta| < \delta_m + \rho_s - \rho_m\)
A total solar eclipse occurs if \(\rho_m > \rho_s\) and the following condition holds.
\(|\delta| < \delta_m + \rho_m - \rho_s\)
Lunar Eclipses
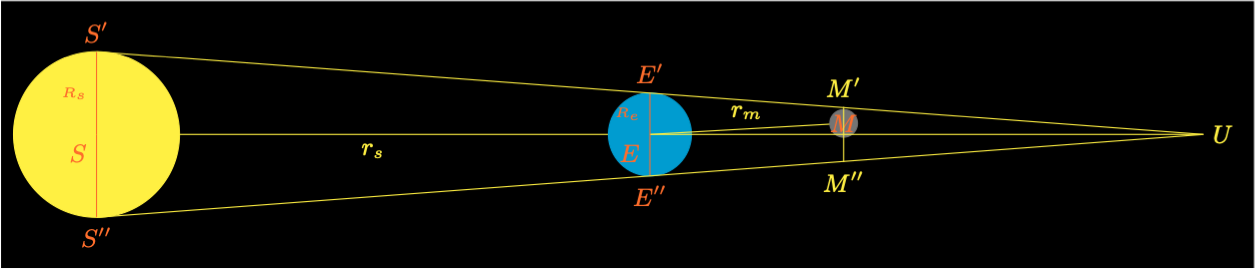
The Earth’s umbra is defined by the cone \(E''UE'\). Define the distance from the vertex of the umbra code to the Earth \(u = UE\) and the half angle of the cone \(\theta = EUE'\). The radius of the umbra at the Moon’s position is \(r_u = MM'\).
We can determine \(u\) from the first two values.
Now, \(R_u\) can be determined from the second two values.
The angular radius of the umbra at the Moon.
The condition for a partial lunar eclipse is:
The condition for a full lunar eclipse is:
The Earth’s penumbra is defined by the cone \(E''U^*E'\). Define the distance from the vertex of the umbra code to the Earth \(p = U^*E\) and the half angle of the cone \(\phi = EU^*E'\). The radius of the umbra at the Moon’s position is \(r_p = MM^*\).
We can determine \(p\) from the first two values.
Now, \(R_p\) can be determined from the second two values.
The angular radius of the penumbra at the Moon.
The condition for a penumbral lunar eclipse is:
For more information see Astro-Mathematics.
